3-4: Ensemble learners - bagging and boosting
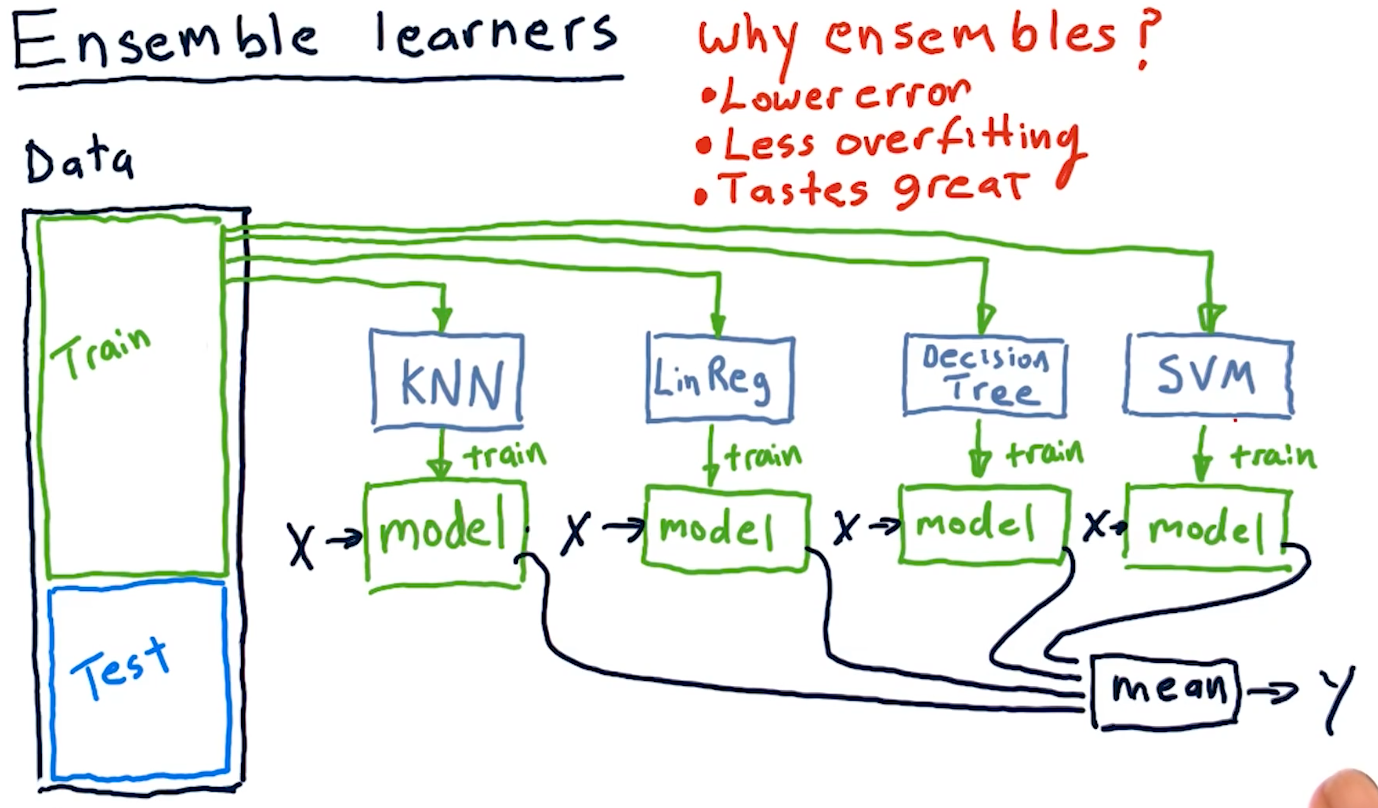
Ensemble learners
Creating an ensemble of learners essentially means that we leverage multiple
different machine learning algorithms to produce a series of different models.
For regression-based learning, we provide each produced model an x and
take the mean of their y responses. Why use ensembles? Ensembles provide:
- Lower error
- Less overfitting
- Removal of algorithmic bias
A diagram representing this concept is provided below:
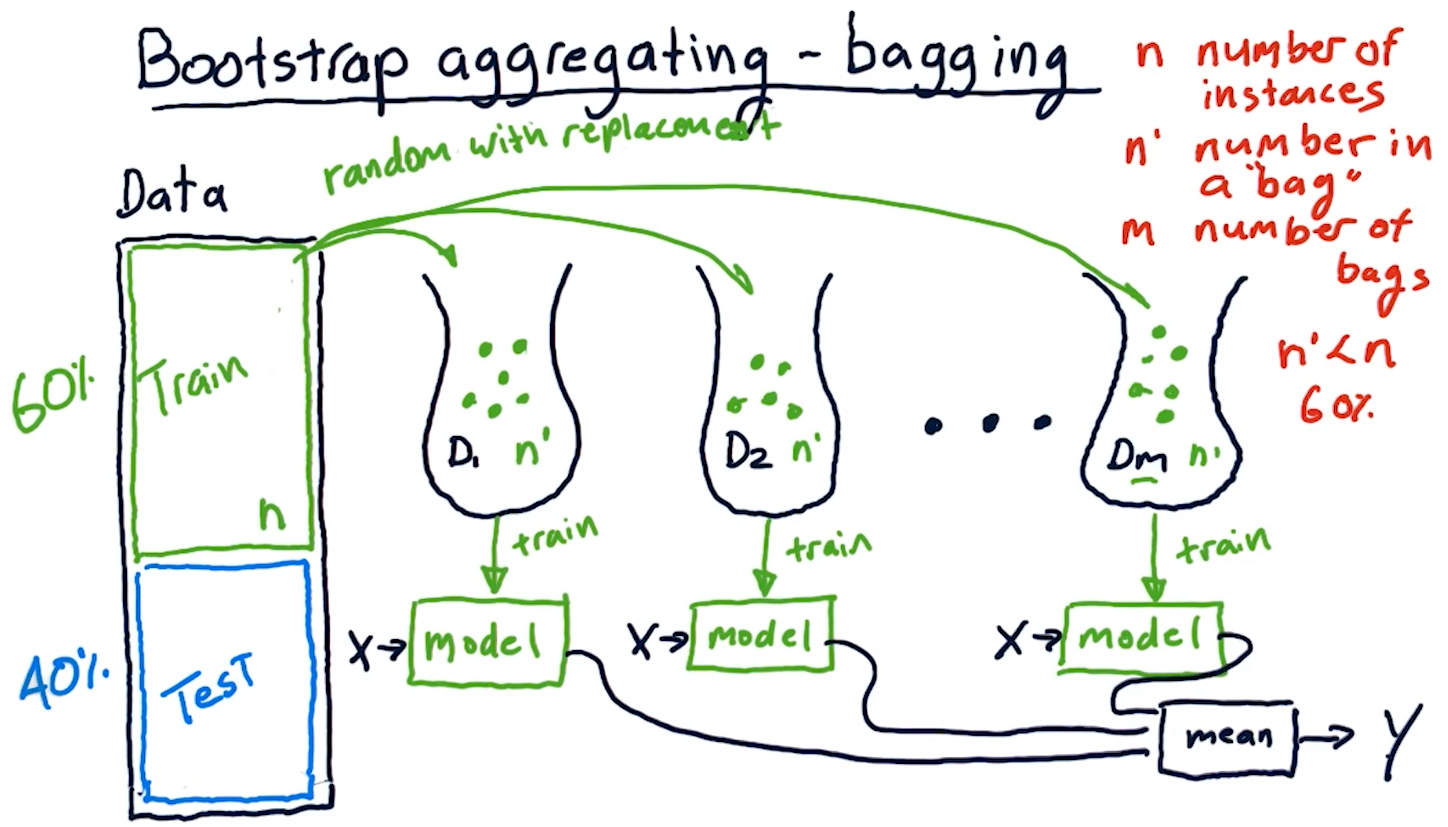
Bootstrap aggregating-bagging
Bagging is a method of creating an ensemble of learners, however, we
utilize the same learning algorithm to create m number of bags and models.
What is a bag? A bag is a set of data derived from the original training
data for a learning algorithm, with up to n' items. n' will always be some
subset of n - usually 60%. The n' items selected from the original data are
random with replacement - we can have duplicate items selected from the
original data.
After we create our m bags with n' number of items, we use these bags to
train our models with the same learning algorithm. Like our ensemble before, we
take the mean of the models' predictions to generate our y.
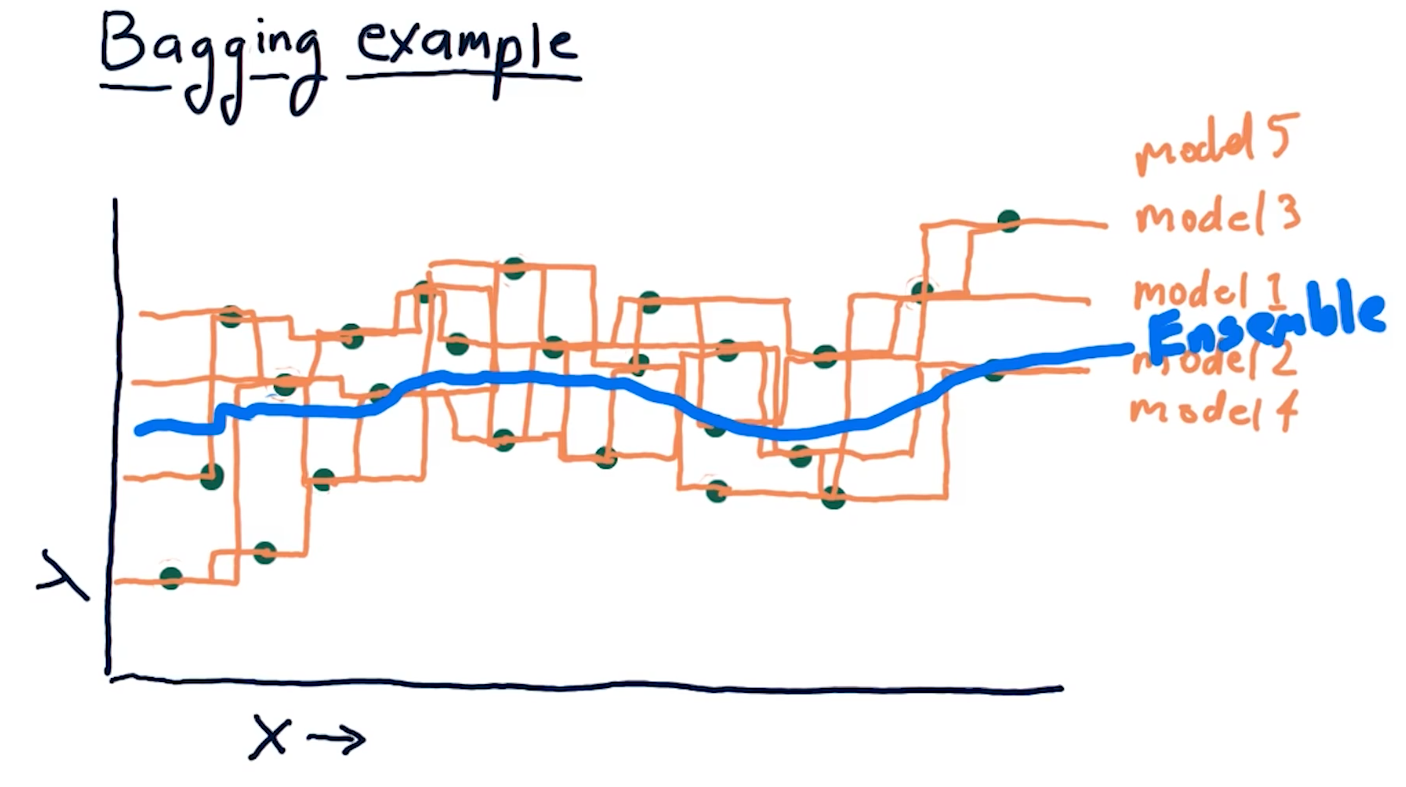
Bagging example
The example diagram provided below demonstrates how an ensemble of 1NN-generated models, using a different subset of random data for each model, generates a much more smooth predictive line than a single 1NN-generated model. Recall that 1NN-generated models overfit the data, however, if we combine these overfit models into an ensemble, the mean prediction provides better correlation with the data.
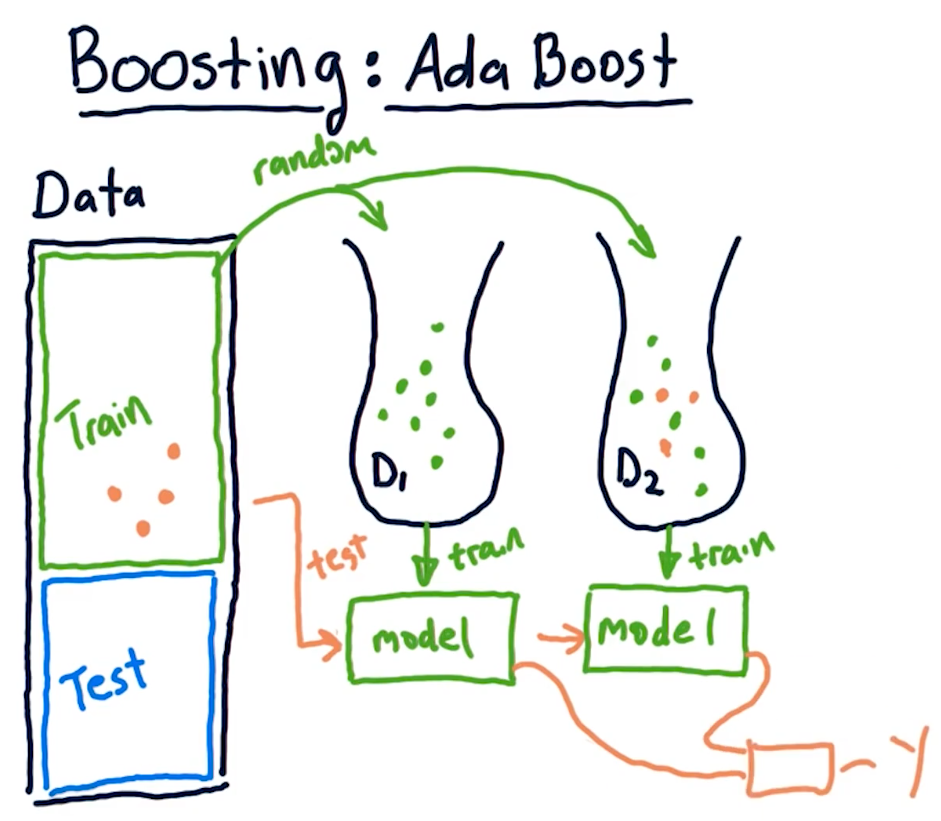
Boosting: adaptive boost
Boosting is a technique similar to bagging, however, it aims to provide weight to particular sections of data in the training data set that may be poorly predicted. Boosting conducts the following actions:
- Select random values from
nto generate a bagmofn'values - Train a model and test the model against the original data within
n - Identify
x, ypredictions from this model that performed poorly - Generate new model with
n'values that are weighted towardnvalues with poor predictions - Train a model with the weighted data and generate more
x, ypredictions - Calculate the mean of
ywith the old and new models - Iterate over this procedure
mtimes