1-8: Optimizers

This lesson covers optimizers, algorithms that can do the following:

• Find the minimum values of functions
• Build parameterized models based on data
• Refine allocations to stocks in portfolios

To use an optimizer, we conduct the following steps:

1. Provide a function to minimize
2. Provide an initial guess of what the minimal outcome is
3. Call the optimizer repeatedly until we reach the minimum

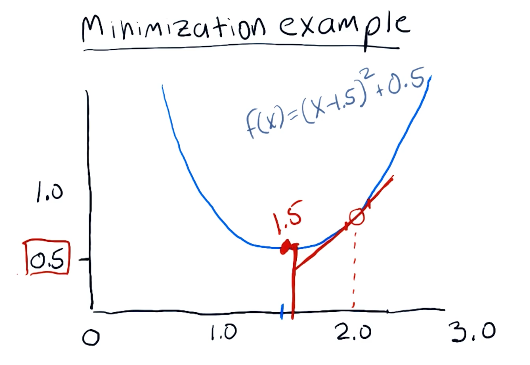
Minimization example

The following example for minimization is provided by the lecture. The minimizer in this example continues to test values for the given equation, tracking the minimum value until it reaches the lowest possible number. This algorithm rejects values that are high than it's most recent minimum, and continues to search for the lowest possible value with greater granularity as it completes iterations of the minimization algorithm.

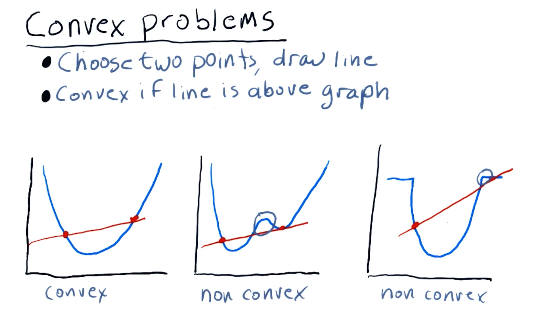
Convex problems

When finding the minima of a given equation, we can run into an issue for complex equations or convex problems. In these problems, the minima can be difficult to find for a traditional minimizing algorithm due to the odd shape of the equation when graphed. It can have local minima, or portions of the line that plateau. Below is a slide from the lecture demonstrating this problem and how a minimization algorithm could solve it:

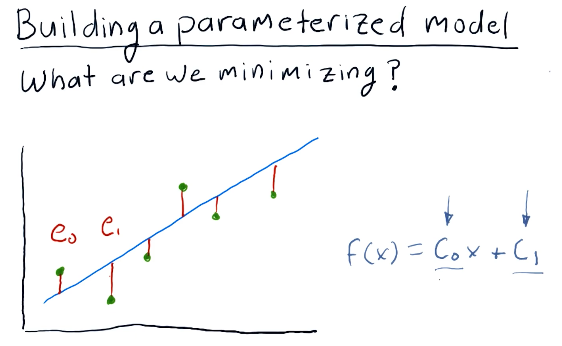
Building a parameterized model

Given a scatterplot like the one shown below from the lecture, a minimizer can determine the coefficients for a given equation by minimizing the distance of a graphed line (from the equation) to the dots on the scatterplot. This distance is known as error. The minimizer will attempt to minimize the amount of error, finding the appropriate coefficients.