2-9: The fundamental law of active portfolio management
Grinold's fundamental law
This fundamental law of active portfolio management describes performance in the terms of skill and breath. These two factors create a ratio wherein you can increase your performance as an active portfolio manager by increasing your skill or you can increase the number of opportunities to test your skill. A slide from the lectures is provided below:

Coin flip casino
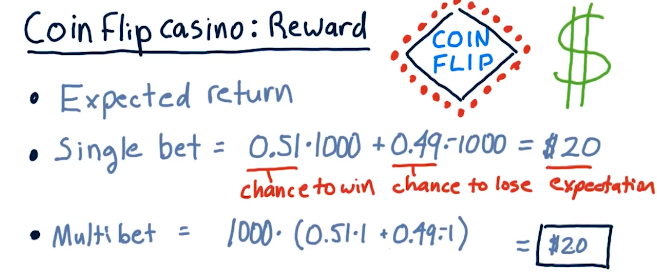
This lecture discusses some scenarios using a coin flip casino, where risk and reward are compared for different betting strategies on the flip of a coin. Fortunately for us, we know that the coin has a 0.51% chance of landing on heads.
The two betting options are:
- Bet $1000 on one coin flip
- Bet $1 on one-thousand coin flips
Obviously, betting $1 on one-thousand coin flips is the best option - this lecture uses this teaching point to demonstrate calculating expected value, probability, and risk via standard deviation.
Expected value
Probability

Standard deviation

Sharpe ratio

Observations
Going back to Grinold's fundamental law, if we take the sharpe ratio of the multi-bet and the single-bet and the number of bets, 1000, we encounter that this follows Grinold's fundamental law. See below for evidence from the lecture:
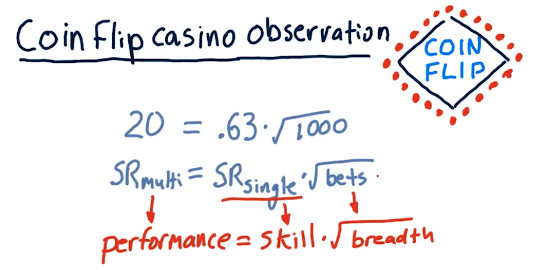
So the following are some good observations:
- Sharpe ratio grows as the square root of breadth increases.
- Sharpe ratio grows as alpha increases.
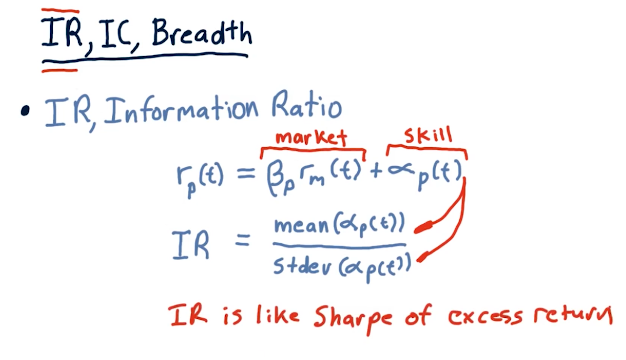
Information ratio
Information Ratio (IR) is like the sharpe ratio for excess return, alpha. The equation broken down is in the lecture slide below:
Information coefficient and breadth
Information coefficient (IC) is the correlation of an active manager's forecasts to returns. Breadth (BR) is the number of trading opportunities per year.