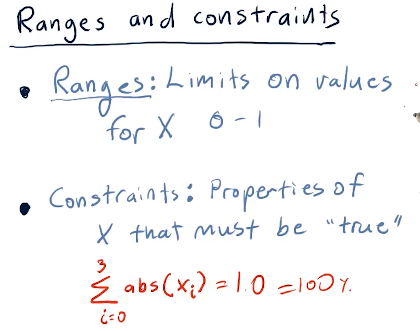1-9: How to optimize a portfolio
What is portfolio optimization?
Given a set of assets and a time period, find an allocation of funds to assets that maximizes performance.
What is performance?
We can choose from a number of statistics such as:
- Cumulative returns
- Volatility or risk
- Risk adjusted returns (Sharpe ratio)
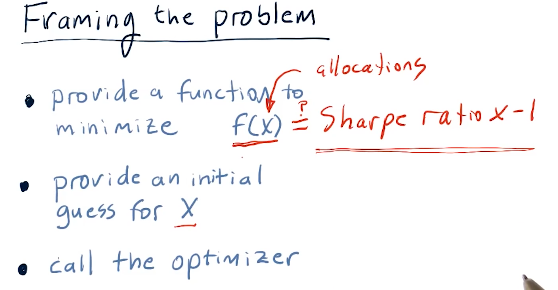
Framing the problem
So how do we go about optimizing a portfolio? We use an optimizer to find the inverse Sharpe ratio for a given set of allocations in a portfolio. A high-level representation provided by the lecture is provided below:
Ranges and constraints
Ranges and constraints on the values of X provided to the optimizer for the
function to be minimized can help speed-up the rate at which the optimize can
solve the minimization of the function. Ranges in this case should be
limited from 0 to 1 as these represent percentages. Constraints in this
example specify that the sum(x) should equal 100 - meaning our allocations
reach 100% for an effectively optimized portfolio. Below is the slide from the
lecture discussing this topic: