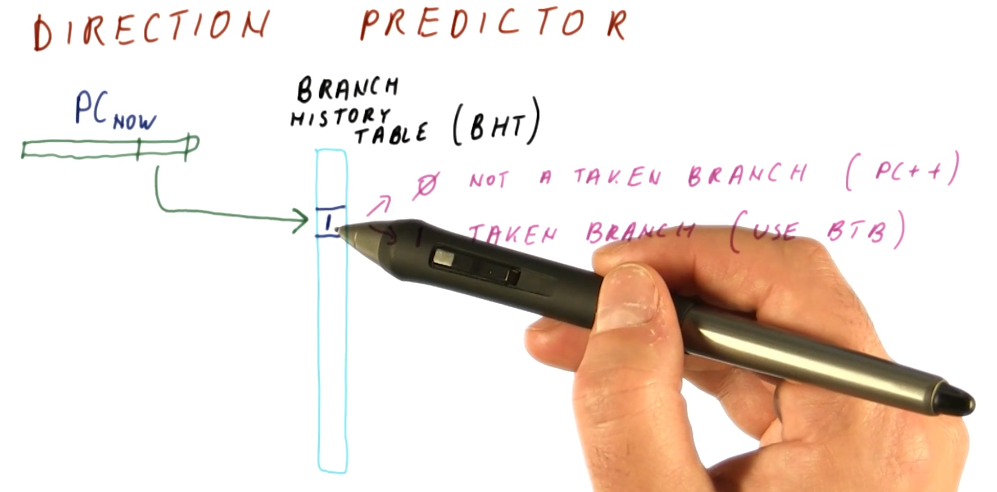
Direction Predictor

We further simplify our branch predictor by adding another abstraction, the branch history table. This table contains a 1 or 0 for each different program counter that indexes into it - we calculate indices just like we did with the BTB (using the LSBits of a program counter that are most likely to be unique).

The 0 represents that the branch is not taken. The program counter is incremented and we begin fetching instructions from that location. No changes are made to the BTB because no branch was taken.

The 1 represents that the branch is taken. The BTB is referenced to determine the next program counter based upon the current one being inspected, and we begin to fetch instructions from that new location.

If the prediction made is incorrect, the branch history table is updated with the correct value at the index - 0 or 1. If a not taken prediction was made and this prediction ended up being incorrect, we update the BTB with the next program counter that is the destination of the branch.

Because the branch history table is only 1 bit for each index, we can have way more entries for unique program counters. This way, we can use the BTB only for branches and not just regular instructions.

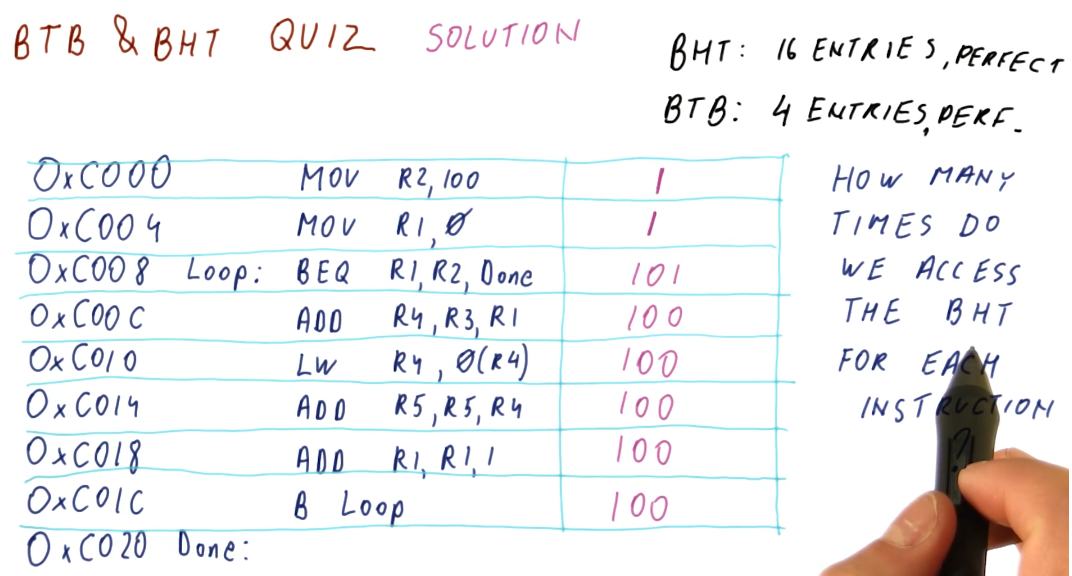
BTB & BHT Quiz

The below quiz excerpt demonstrates that the BHT needs to be accessed for each instruction.

BTB & BHT Quiz 2

The below quiz excerpt demonstrates how the BHT is indexed using the program counter.

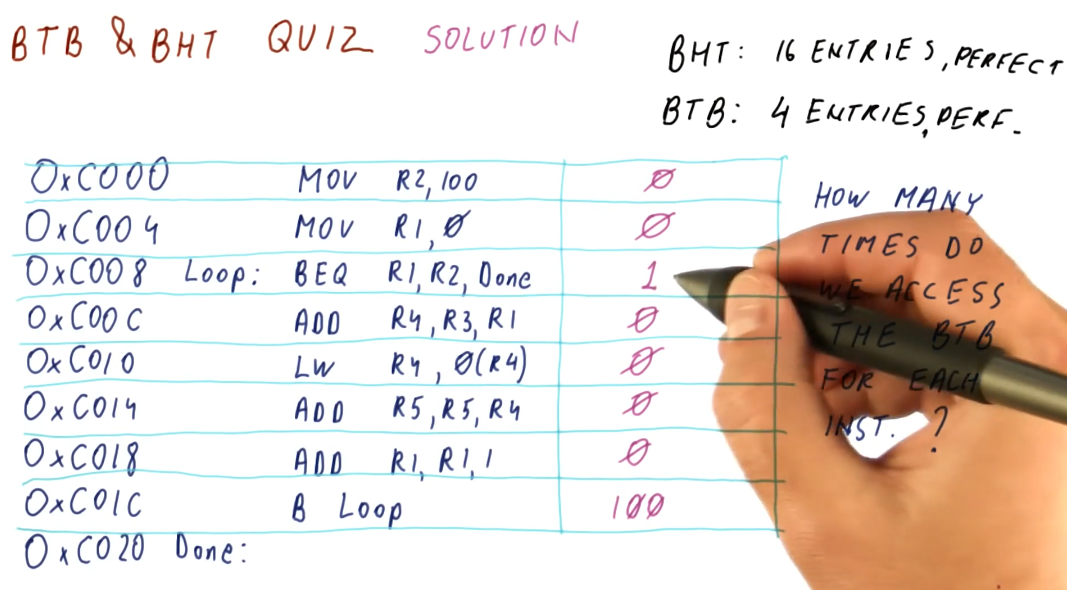
BTB & BHT Quiz 3

The below quiz excerpt demonstrates the conditions required to access the BTB.

BTB & BHT Quiz 4

The below quiz excerpt demonstrates how the BTB is indexed using the program counter.

BTB & BHT Quiz 5

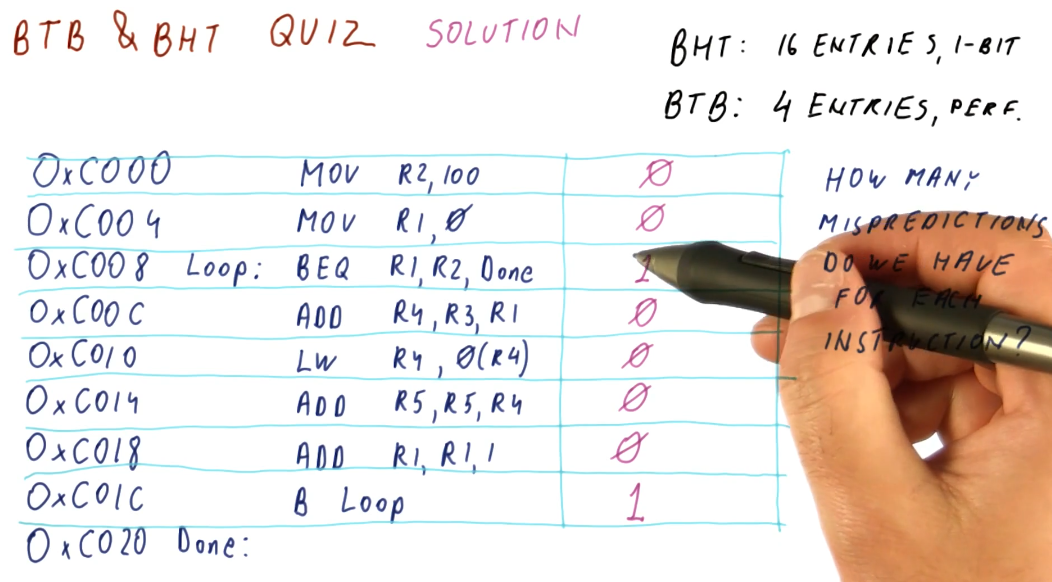
The below quiz excerpt demonstrates how we can calculate the number of mis-predictions for each instruction using an imperfect BHT.

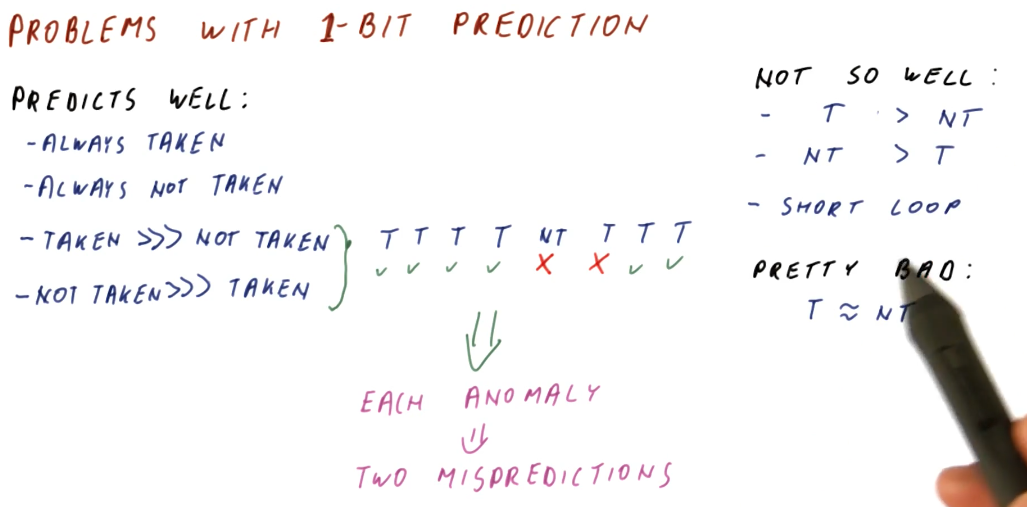
Problems with 1 bit prediction

So what's wrong with the 1 bit predictor? Why does its performance not satisfy the needs of computer architecture designers, creating the need to research pattern predictors?

The 1 bit predictor predicts these things well:

• Branches that are always taken
• Branches that are always not taken
• Branches that are taken A LOT more often than not taken
• Branches that are not taken A LOT more often than taken

The example below demonstrates how, when a 1 bit predictor encounters an anomaly in predictions for a particular branch, this can incur two mis-predictions.

The 1 bit predictor does not perform well when:

• Branches are taken more often than not, but not by much
• Branches are not taken more often than not, but not by much
• Encountering short loops

The 1 bit predictor will be bad when:

• Branches taken and not taken are about the same in number